

Similarly, for the intersection of $A_1$ and $A_2$, let $v_1=y_1-3$ and $v_2=y_2-4$, so you get $v_1+v_2+y_3+y_4=5$ with all variables non-negative. After reading the two previous sections, youre probably wondering why we stated the Principle of Inclusion-Exclusion in such an abstract way, as in those examples N(S) N ( S) depended only on the size of S S and not its contents. So for PEV's $A_1$, let $v_1=y_1-3$, then you have $v_1+y_2+y_3+y_4=9$ and the variables are non-negative, so the previous paragraph applies.
#INCLUSION EXCLUSION PRINCIPLE HOW TO#
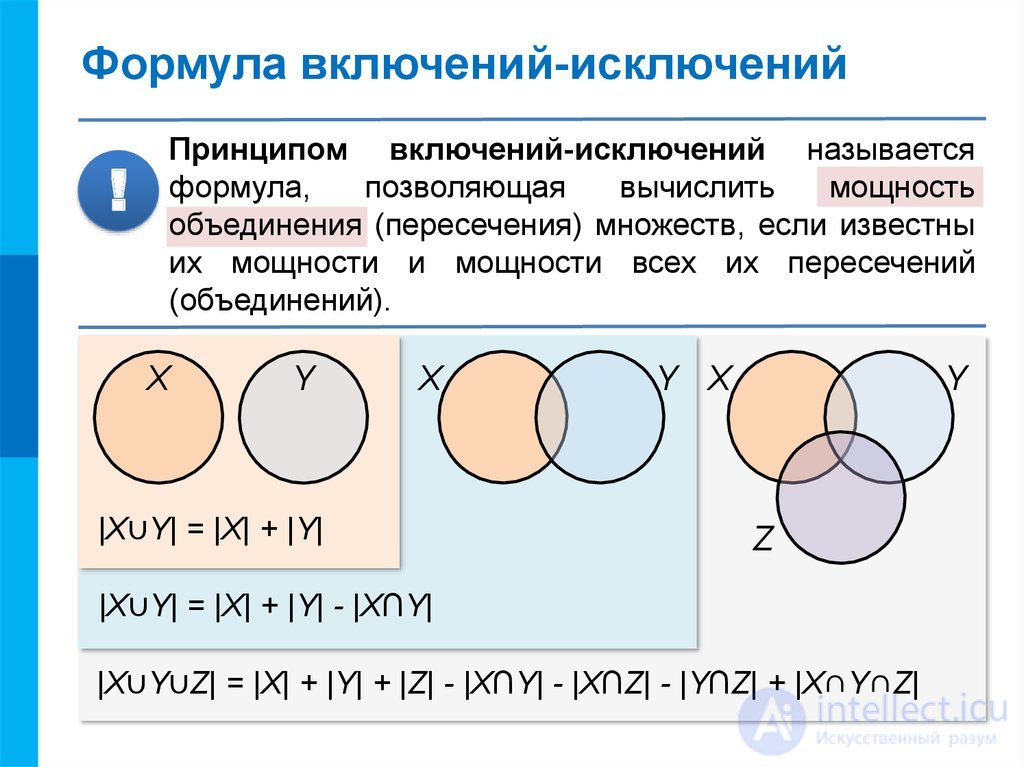
It isn't clear whether you mean that you don't see how to get a formula for the size of the union by using inc-excl, or whether you mean that you can write down a formula but don't see how to find the sizes of the $A_i$ and the various intersections that arise, so it's a little hard to help you here. Then you ask how to use inclusion-exclusion. Thus the goal of this note is to give an insight into the shape of this formula which students and users of nite elds may nd helpful. So the question becomes, how many ways can you choose which $r-1$ of the $n+r-1$ dots to circle? Unfortunately, PEV wrote 18-choose-3, where I think what's wanted is 15-choose-3, but now you should see how to get that part of the answer. The uncircled dots are $n$ in number, and the circled ones divide the uncircled ones into $r$ groups (some of which may be empty), so you get $r$ non-negative integers adding up to $n$. Imagine $n+r-1$ dots in a line, and circle $r-1$ of them. As for the remarks about the Inclusion-Exclusion Principle and the algorithm, I interpreted them as calls for alternative solutions. Questions that do not include that information tend to be closed. You need to know the number of solutions of $$u_1+u_2+\dots+u_r=n$$ when the only restriction on the variables is that they be non-negative integers. However, you are much more likely to obtain helpful responses if you tell us what you have attempted and explain where you are stuck. I'm not sure I can expand on PEV's hints in a comment, so I'll make it an answer. Those natural numbers that are coprime with the number are not divisible by any of the primes 1. But that's the exercise, figuring out how to manage including/excluding/then including back of what you threw away too much of /then excluding back again that littlest bit messed up in that last step. Thus, we have just proved the principle of inclusion and exclusion. To demonstrate the validity of this relation, we will use the inclusion-exclusion principle 12. Study-specific variables: Type and stage of disease, previous treatment history, presence of chronic conditions, ability to attend follow-up study appointments, technological requirements (e.g., internet access) Control. Now it gets harder, because you need to do it for 4 variables not just 2. Examples of common inclusion and exclusion criteria are: Demographic characteristics: Age, gender identity, ethnicity. How many solutions where $0\le x_1\le 5$, $0\le x_2\le7$? Hint: exclude the both complements, but re-include where those two complements overlap (the intersection of those two excluded ranges - what is it), because you excluded the intersection twice. How many solutions where $0\le x_1\le 5$, $0\le x_2$? Hint: exclude the complement. How many solutions where $6\le x_1$, $6\le x_2$? (these last questions don't really say anything about inclusion-exclusion yet) The formula which gives the number of objects not having any of the m properties is called the principle of inclusion and exclusion, and was discovered about. How many solutions where $6\le x_1$, $0\le x_2$? How many solutions where $0\le x_1$, $0\le x_2$? How many solutions to $x_1 + x_2 = 15$, no restrictions? (infinite of course) 263-266.If you don't get the larger question, start smaller first. The inclusion-exclusion principle states that the number of elements in the union of two given sets is the sum of the number of elements in each set, minus the number of elements that are in both sets. RIEČAN, B.: A descriptive definition of the probability on intuitionistic fuzzy sets, in: Proc. Štépnička, et al., eds.), Universitas Ostraviensis, Ostrava, 2007, pp.
RIEČAN, B.: M-probability theory on IF-events, in: New Dimensions in Fuzzy Logic and Related Technologies, Proc. KUKOVÁ, M.: The Inclusion-Exclusion Principle for IF-events, Inform. KELEMENOVÁ, J.: The inclusion-exclusion principle in semigroups, in: Recent Advances in Fuzzy Sets, IF-Sets, Generalized Nets and Related Topics, Vol. In this chapter we discuss a method of counting which has been used for at least 300 years.

GRZEGORZEWSKI, P.: The inclusion-exclusion principle for IF-events, Inform. CIUNGU, L.: The inclusion-exclusion principle for IF-states, Inform. WILF ’09, Palermo, Italy, Lecture Notes in Comput. CIUNGU, L.-RIEČAN, B.: General form of probabilities on IF-sets, in: Proc.


 0 kommentar(er)
0 kommentar(er)
